The Mathematics Behind "Ride the Bus"

When I got to college a friend introduced me to a drinking game called "Ride the Bus." The rules for the full game are here, but I was interested in the final section. For that section, there are four questions. For the first card, is it red or black? For the second card, is it higher or lower than the first card? For the third card, is it in between (inclusive) or outside of the first two cards? And for the fourth card, what suit is it? You continue pulling cards until you get all four in a row right. If you get any one wrong you drink, and start over.

Now time for the analysis. First off, I'm assuming that you're playing like most people play drinking games, a.k.a. without the ability to remember every card already shown. I'm assuming that you're making the most educated guesses you can without knowing what other cards have appeared. Additionally, I'm playing the way I was taught, which is that the game doesn't end when you run through all 52 cards in the deck, you reshuffle and keep going until you win. With that in mind, how many drinks should you expect to drink, and how many cards are you expected to go through?

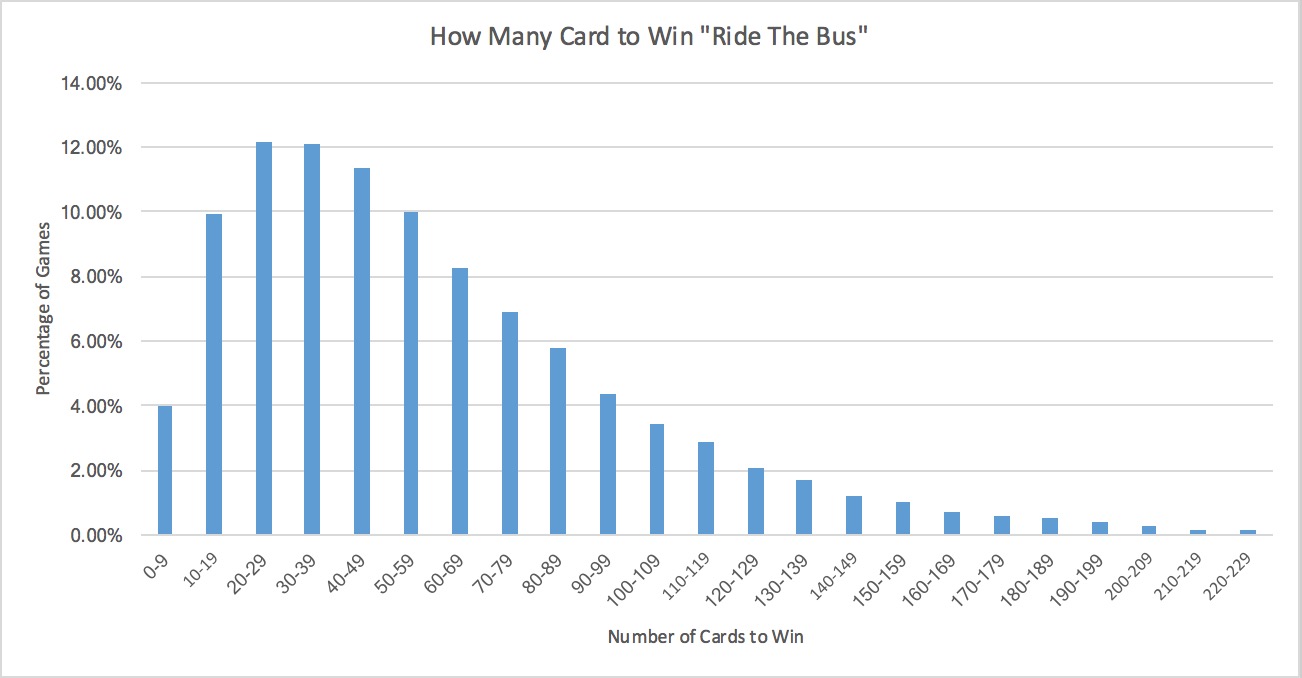
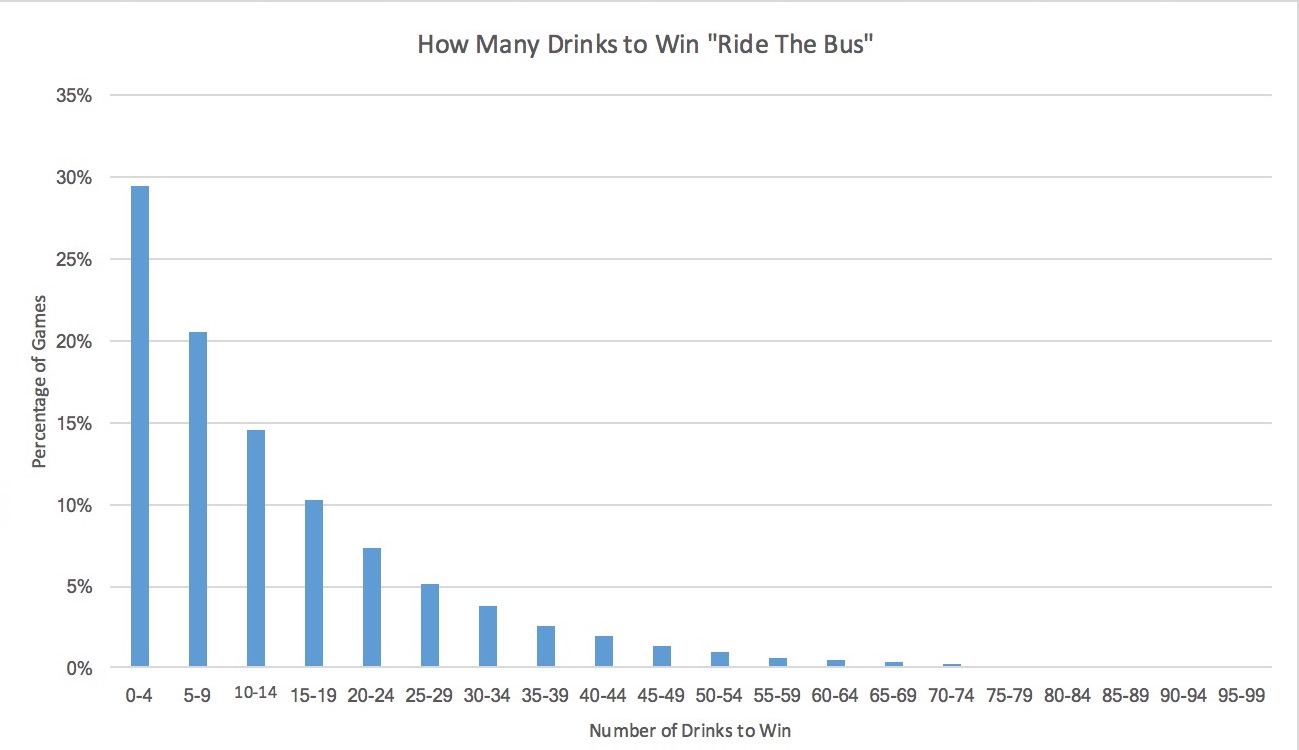
This is a problem that could have been solved with some paper and pencil and some thought about the statistics behind it. Or you can write the game in Python and play it 100k times. I went with the second option. Here are the results:

And for some of the less formatted data points. The average game goes through 32 cards and results in 14 drinks. Some of the steps are as you would expect: the chance of guessing red vs. black is 50%, and guessing the correct suit is 25%. Over under is also findable with some more complex statistics, and has a success rate of 75%. The third correct is a little more tricky, but the testing gave it a success rate of 71%.

Because the game is technically possible to never finish, there is no ceiling to the number of drinks/cards you can go through. That being said, in my 100k tests the highest number of drinks was 122, with the highest number of cards of 259.

But this is all for a typical human player. What about the perfect strategy? If you can remember every card that's been played the statistics change. Let's go through each improvement piece by piece. If you can remember the red/black color count, the average number of drinks drops to 12.5, and the number of cards drops to 30. Your chance of getting the first card correct rises to 55%. If you're doing over-under optimally, your percentage rises to 76%, having a negligible effect on drinks/cards. If You're doing inside-outside optimally, your percentage rises to 72% again having a negligible effect. If you optimally guess the suit, your percentage rises to 32%. That has a pretty significant effect.

Overall, if you're using the optimal strategy you'll go through 24 cards and have 9.5 drinks, which is a 25% drop in cards, and a 32% drop in expected drinks. In the end though, if you're playing "Ride the Bus" you're not trying to minimize your alcohol intake. You're just along for the ride.

Note:
You can find the Excel document for the dumb player here.
You can find the code that I used here.